Boosting Matrix Multiplication Speed and Flexibility with NVIDIA cuBLAS 12.9

The NVIDIA CUDA-X math libraries empower developers to build accelerated applications for AI, scientific computing, data processing, and more.

Two of the most important applications of CUDA-X libraries are training and inference LLMs, whether for use in everyday consumer applications or highly specialized scientific domains like drug discovery. Multiple CUDA-X libraries are indispensable for efficiently training LLMs and performing inference tasks with groundbreaking performance on the NVIDIA Blackwell architecture.

cuBLAS is a CUDA-X library that provides highly optimized kernels for performing the most fundamental linear algebra tasks, like matrix multiplications (matmuls), which are crucial for LLM training and inference.

The newly available cuBLAS in NVIDIA CUDA Toolkit 12.9 supports new features that further optimize cuBLAS matmul performance. It also enables greater flexibility to balance needs like accuracy and energy efficiency by tuning floating point precision and leveraging the building blocks of emulation.

This post shows how cuBLAS 12.9:

Introduces new FP8 scaling schemes for NVIDIA Hopper GPUs that provide flexibility and performance.
Leverages block-scaling available with NVIDIA Blackwell fifth-generation Tensor Cores for FP4 and FP8 matmuls.
Accelerates matmuls across various precisions, including FP4, which reaches up to 2.3x and 4.6x over FP8 matmuls on Blackwell and Hopper GPUs.
Enables FP32 emulation with Blackwell BF16 tensor cores that can run matmuls 3x to 4x faster than Blackwell and Hopper native FP32 matmuls while improving energy efficiency.

Channel- and block-scaled FP8 matmuls on NVIDIA Hopper

Scaling is fundamental to maintaining accuracy in training and inference when matmuls are performed using narrow data types (such as FP8). Previous cuBLAS versions enabled FP8 tensor-wide scaling (single scaling factor) on NVIDIA Hopper and NVIDIA Ada GPUs. Now, cuBLAS 12.9 enables greater flexibility for several new scaling schemes on Hopper GPUs.

The first is channel-wide or outer vector scaling, enabling a single scaling factor to apply to individual matrix rows of A_[MxK] or columns of B_[KxN]. This can be extended further with block scaling, which applies a scaling factor to each 128-element 1D block within the K dimension, or a 128×128 2D block, of matrices A and B.

Using 1D blocks enables better accuracy, and 2D blocks provide better performance. cuBLAS supports different scaling modes for A and B (1D x 1D, 1D x 2D, and 2D x 1D).

A benchmark for large matmuls of various sizes is presented in Figure 1. Using the various FP8 scaling schemes can provide up to a 1.75x speedup, and, in all but one case, the FP8 scaling schemes provide at least a 1.25x speedup over the BF16 baseline.

A bar chart of the speedups provided by the three new FP8 scaling schemes and the previous tensor-wide scaling, compared to a baseline BF16 for a range of matmul sizes. — *Figure 1. Benchmark comparing different FP8 scaling schemes to a BF16 baseline for various matmul sizes on an H200 GPU (input matrix dimensions are defined as A_[MxK]B_[KxN])*

For usage examples, refer to the cuBLASLt Library API examples.

Block-scaled FP4 and FP8 matmuls on NVIDIA Blackwell

NVIDIA Blackwell Tensor Cores introduce native support for finer-grained 1D block-scaled FP4 and FP8 floating-point types, which provides a new level of balance between reduced precision and throughput. This method enables more precise representation of values within each block, for improved overall accuracy compared to using a single global scaling factor.

cuBLAS 12.9 can make use of these new precisions with the following cuBLASLt APIs, where `E` is the exponent defining the dynamic range of the number and `M` is for the mantissa precision:

`CUDA_R_4F_E2M1`: matmuls with `CUDA_R_UE4M3` scales and 16-element blocks. The scaling type is a variant of `CUDA_R_E4M3` with the sign ignored. See the API example.
`CUDA_R_8F` variants: matmuls with `CUDA_R_UE8` scales and 32-element blocks. Here, the scaling type is an 8-bit unsigned exponent-only floating data type, which can be thought of as FP32 without the sign and mantissa bits. See the API example.

The diagram shows how inputs, (de)quantizations, scaling factors, and outputs tie together for the new FP4 and FP8 block-scaled datatypes. — *Figure 2. Diagram of a block-scaled GEMM with epilogue, scaling factors, and multiple outputs supported by the cuBLASLt API*

Furthermore, thanks to the small block size, with the new scaling modes, cuBLAS matmul kernels can compute scaling factors for the D tensor (scaleD in Figure 2) when the output is FP4 or FP8. This removes the need to estimate the scaling factor or make additional passes over data before performing a conversion, which is necessary for tensor-wide scaling.

Note that when D is an FP4 tensor, there is a second-level scaling factor applied to all the values before they are quantized. See the explanation of quantization in the cuBLAS documentation for more details.

cuBLAS 12.9 matmul performance on NVIDIA Blackwell GPUs

With the new data types, runtime heuristics, and kernel optimizations available in cuBLAS 12.9, users can take advantage of the incredible performance of Blackwell GPUs.

Figure 3 presents the latest matmul performance available in cuBLAS for various precisions, comparing NVIDIA B200 and GB200 to Hopper H200. The synthetic benchmarks consist of large, compute-bound matrix sizes (left) and a thousand random matrix sizes (right) that span latency-bound to memory-bound, and to compute-bound sizes.

The random matrix dataset consists of smaller matrices that make matmul performance dominated by bandwidth ratios, resulting in speedups that are less than the compute-bound cases. In the compute-bound case, block-scaled FP4 is 4.6x faster on the GB200 than the H200 FP8 baseline, achieving up to an absolute performance of 6787 TFLOPS/s.

This chart shows the geomean speedups of matmuls (A[MxK]B[KxN]) in various precisions on Blackwell compared to Hopper, confirming that cuBLAS achieves close to the throughput ratios on large, compute-bound sizes. The chart also shows that for a dataset of one thousand random sizes (small to large) and shapes, the speedup is dominated by the bandwidth ratios between Blackwell and Hopper GPUs. — Figure 3. Geomean speedups across precisions for synthetic matrix sizes (left: large, compute-bound sizes; right: a thousand random sizes and shapes) on B200, GB200, compared to H200. Absolute performance in TFLOP/s is also reported for GB200 on the compute-bound matmuls (left)

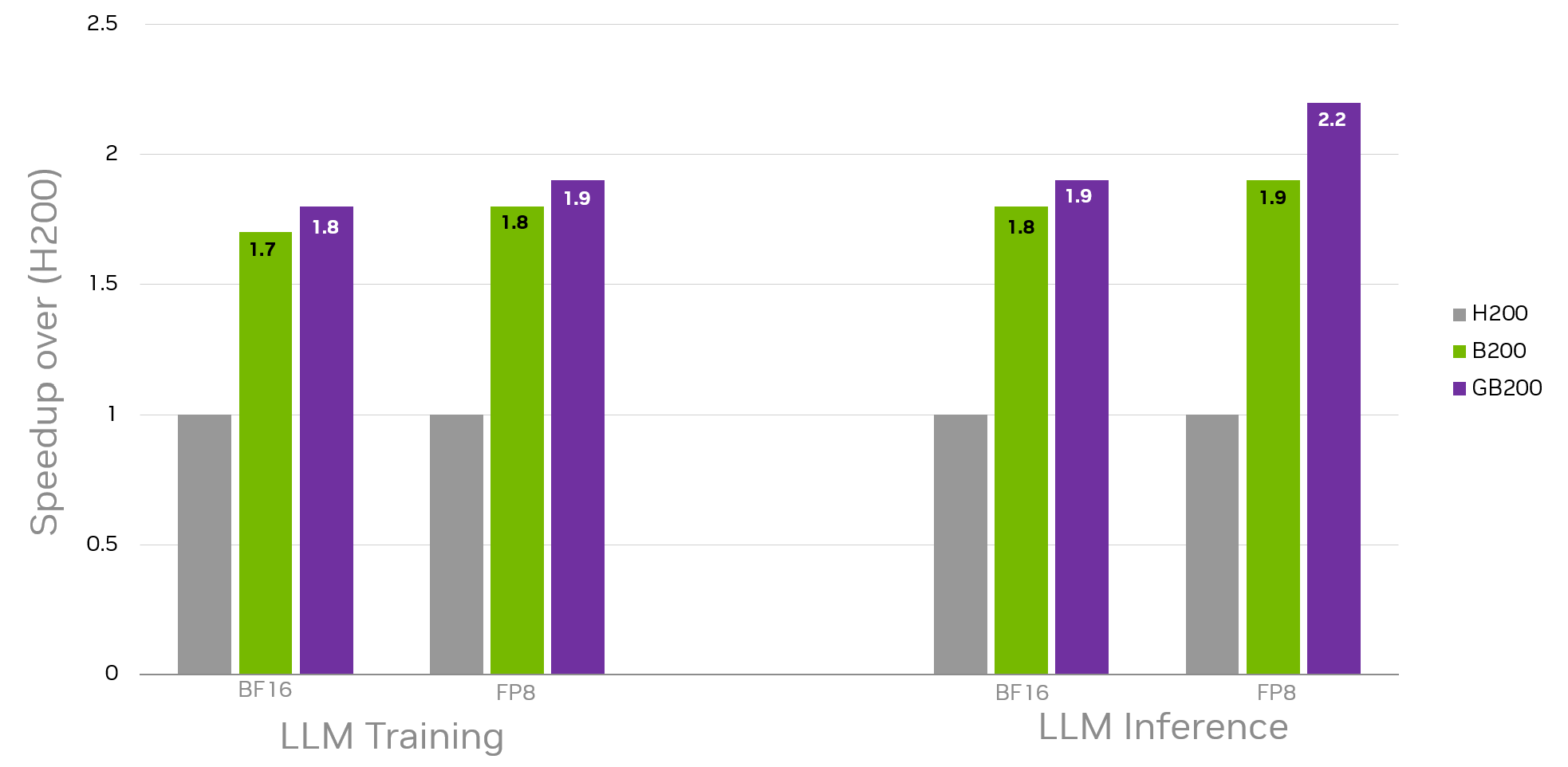
Blackwell architectures also perform well on real-world data sets composed of matmul shapes and sizes that dominate important LLM training and inference workloads (Figure 4), achieving at least a 1.7x speedup and up to a 2.2x speedup over H200 baselines obtained with BF16 and FP8 data types (B200 and GB200). These geomean speedups in Figure 4 are only for the matmuls and their associated repeat counts in each model in the dataset. The final end-to-end speedup depends on the performance of non-matmul fractions of the workloads as well.

This chart shows that a geomean speedup of above 1.5x and up to 2.2x can be expected for an ensemble of important workloads in LLM training and inference today on Blackwell (B200 and GB200) compared to Hopper (H200) GPUs. The precisions dominating these workloads are FP8 (with tensor-wide scaling) and BF16. — *Figure 4. Matmul-only geomean speedups across important workloads in LLM training and inference on B200 and GB200 compared to H200.*

The performance achieved by the Blackwell architectures can be further improved with opportunistic optimization available through cuBLASLt heuristics API and autotuning [6,7].

Speeding up FP32 matmuls using BF16 tensor cores on Blackwell

In addition to the impressive performance that cuBLAS already delivers on Blackwell, it also introduces a feature that enables users to opt in to emulation for potentially faster FP32 matrix multiplications and improved power efficiency.

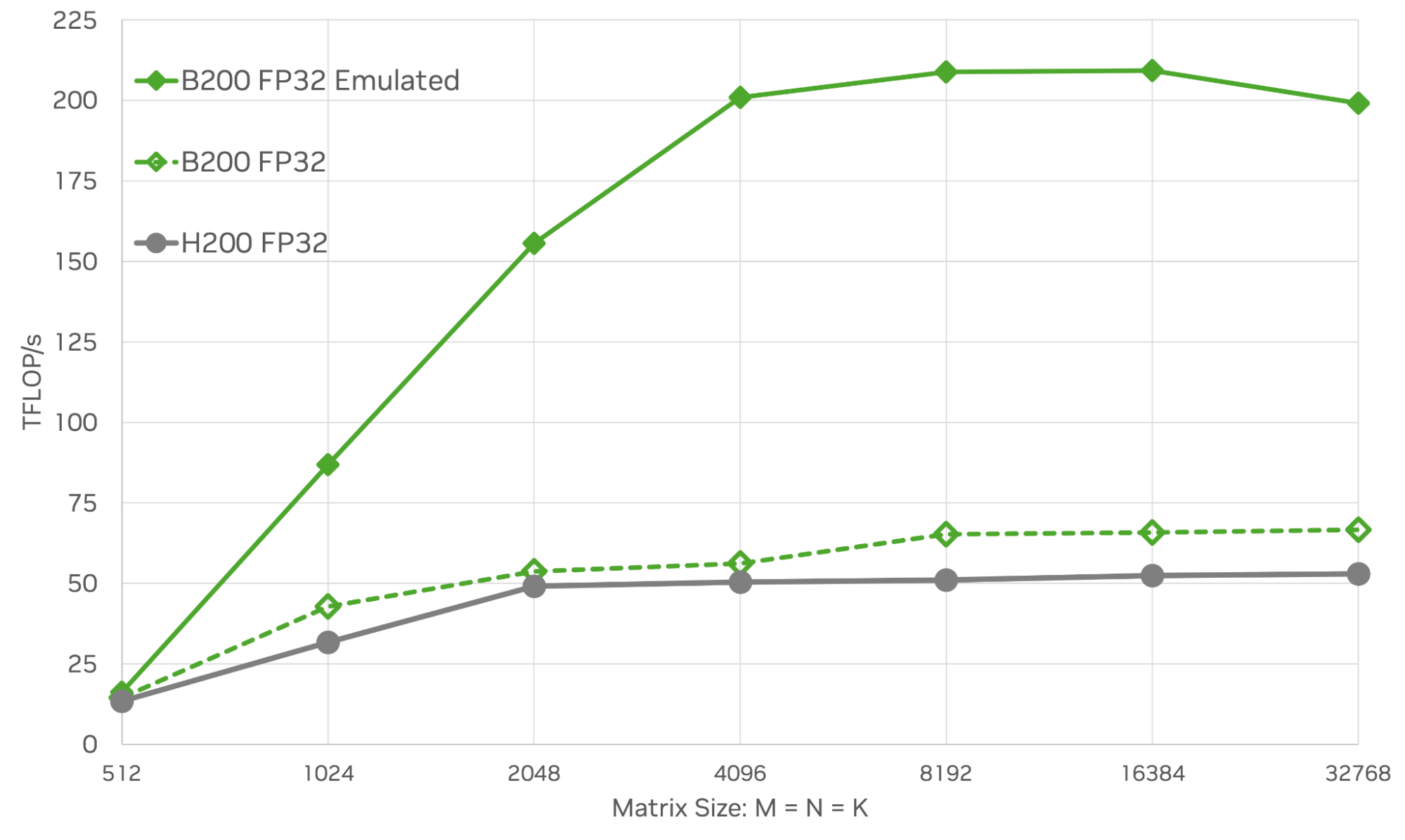
Figure 5 demonstrates the FP32 emulation performance available on B200 GPUs compared to native FP32 performance and H200 GPUs for various square matrix sizes. In the largest case (M=N=K=32,768), emulation achieves between 3 and 4x more TFLOPS than native FP32 on B200 or H200.

The chart shows that up to 3x and 4x speedup is available versus the native FP32 throughput on Blackwell and Hopper, respectively. The chart reports performance in TFLOP/s for B200 and H200 GPUs. — *Figure 5. Performance (TFLOP/s) of emulated FP32 compared to native FP32 on B200 and H200 GPUs*

Emulation of matmuls for scientific computing applications is now well understood, and several algorithms and implementations that leverage emulation to boost performance and energy efficiency are available.

For example, the NVIDIA GTC 2025 talk How Math Libraries Can Help Accelerate Your Applications on Blackwell GPUs demonstrates a key component of a weather forecasting application where emulation provided a 1.4x performance and a 1.3x energy efficiency improvement.

The current implementation of FP32 emulation in the cuBLAS library leverages the BF16 tensor cores. For usage examples, please refer to the cuBLASLt Library API examples. The emulation of matmuls in FP64 is currently under development.